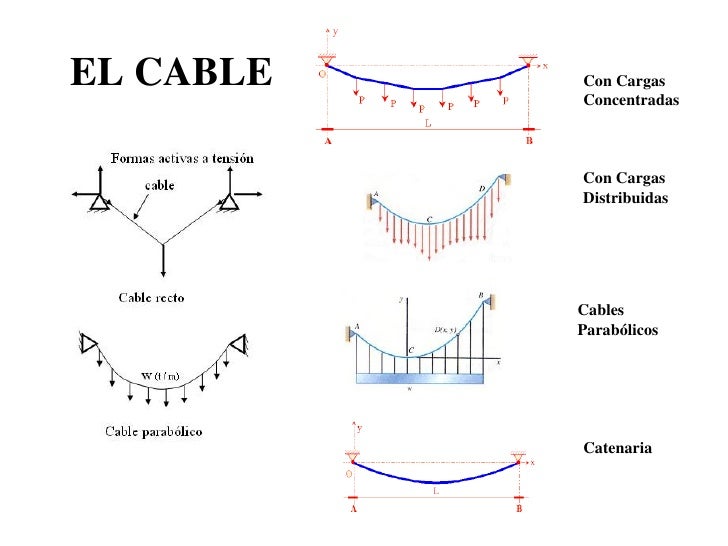
CABLES SUSPENDIDOS
Los cables a menudo son usados en estructuras ingenieriles para soportar y transmitir cargas de un miembro a otro. Cuando se utilizan para soportar puentes colgantes y ruedas de tranvía. Los cables constituyen el elemento principal de carga de la estructura.
Es decir , son considerados uno de los elementos esenciales para cualquier forma estructural en el área de ingeniería y arquitectura, son elementos flexibles debido a sus dimensiones transversales pequeñas, en relación con su longitud, logrando así una mayor resistencia a las tensiones que es sometido. Tomando en cuenta las magnitudes que los cables son capaz de soportar por la fuerzas de tracción, son hechos de acero.
Generalmente las formas más usuales donde se pueden observar los cables son en puentes colgantes, puentes estabilizados, ruedas de tranvía, líneas de transmisión, teleféricos, contra vientos para torres altas, entre otros. Los cables suspendidos constituyen el elemento principal de carga de la estructura.
por ejemplos:

CABLE CON CARGAS UNIFORMEMENTE DISTRIBUIDOS A LO LARGO DE LA HORIZONTAL
Cuando un cable
soporta cargas distribuidas, estas se pueden considerar
como cargas concentradas suficientemente próximas,de tal manera que el
cable adquirirá una forma curva(poligonal con infinito número de
lados).Supongamos inicialmente que la carga es uniformemente distribuida a lo
largo de la horizontal, tales el caso de un puente colgante, [Fig. 1].
Fig.1

Sea
w
la carga uniforme a lo largo de la horizontal.
Para determinar la forma que adquiere el cable con este tipo de carga se toma una
porción de cable desde su punto mas bajo hasta un punto de coordenadas
(x,y)

[Fig.1-2]. La tensión en este
punto T será tangente a la curva.Tomando momentos con respecto al punto ( x,y ) se tiene que ,entonces[1-21]que es la ecuación de una parábola,
con origen en el punto más bajo del cable. Con la ecuación [1-2] es
posible determinar el valor de
T
0
, conociendo la posición de un punto
del cable. Para determinar la tensión en cualquier punto, considerando
el triángulo de fuerzas dela porción del cable se tiene que:[1-2]
CABLES PARABÓLICOS
Cuando un hilo está sometido a una carga uniforme por unidad de proyección horizontal, dicho hilo adquiere la forma de una parábola si se desprecia su peso propio respecto al de la carga que debe soportar. Este caso se presenta, en la práctica, en el cálculo de puentes colgantes, en los que el peso del tablero es mucho mayor que el del cable que lo sustenta. En conclusión los cables parabólicos la forma que genera la curva de los cables suspendidos a lo largo de la horizontal es una parábola, de ahí la detonación de su nombre.
El tablero, o base del puente colgante, lo podemos representar por una carga vertical, p (N/m), uniformemente distribuida a lo largo de la proyección horizontal del cable. La transmisión de carga del tablero al cable se realiza mediante unos cables verticales denominados tirantes, también de peso despreciable frente al del tablero.

por ejemplo
Si la distribución del peso(w) es constante, se puede hacer énfasis en las ecuaciones que rigen el comportamiento del cable, obteniendo de esta forma la altura en función del cuadrado de x, es decir, sigue una curva tipo parábola.
La carga por unidad de longitud (medida en forma horizontal) se representa con w y se expresa en N/m o en lb/ft. Seleccionando ejes coordenados con su origen en el punto más bajo C del cable, se encuentra que la magnitud W de la carga total soportada por el segmento que se extiende desde C hasta el punto D de coordenadas x y; y está regida por W=wx.
CABLES EN FORMA CATENARIA
Llamando wpp la carga por unidad de longitud (medida a lo largo del cable), encontramos que la magnitud W de la carga total soportada por una porción de cable de longitud s medida desde el punto más bajo a un punto a lo largo del cable es W = ws.
El modelo de cable por excelencia, ya que aparece en una infinidad de casos en la naturaleza,forma en donde el peso del cable influye en el análisis del peso resultante. Por ejemplo los tendidos eléctricos, una cadena, o una tela de araña son ejemplos de catenaria. En este caso, el cable solo está sujeto a su propio peso. El concepto parece sencillo, sin embargo es el que contiene una mayor carga matemática.
Para determinar completamente la catenaria es necesario conocer su longitud. Para este fin se pueden considerar las tensiones verticales y horizontales siguiendo el siguiente esquema:

Por último, hay que saber determinar la altura en cualquier punto del cable, lo que además es necesario para calcular la tensión vectorial en cada punto. Esta es proporcional a su altura (T = cy).

en el siguiente link se le muestra un ejemplo mas claro
https://prezi.com/vpngvekkbuxm/cables-en-catenaria/
CABLES CON CARGAS CONCENTRADAS
Los cables se utilizan en muchas aplicaciones ingenieriles, tales como puentes colgantes, líneas de transmisión, teleféricos, contra vientos para torres altas, entre otros. Los cables pueden dividirse en dos categorías de acuerdo con las cargas que actúan sobre estos.
Considérese un cable unido a dos puntos fijos A y B y que soportan cargas concentradas verticales P1, P2…….Pn. se supone que el cable es flexible, esto es que su resistencia a la reflexión es pequeña y puede despreciarse. Además, también se supone que el peso del cable es susceptible de ser ignorado en comparación con las cargas que soporta
Por lo tanto, cualquier porción del cable entre dos cargas consecutivas se puede considerar como un elemento sometido a la acción de dos fuerzas y, por consiguiente, las fuerzas internas en cualquier punto del cable se reducen a una fuerza de tensión dirigida a lo largo del cable.
Se supone que cada una de las cargas se encuentran en una línea vertical dada, esto es, que la distancia horizontal desde el apoyo A hasta cada una de las cargas es conocida; además, también se supone que las distancias horizontal y vertical entre los apoyos son conocidas.
por ejemplo


EJERCICIOS
http://documents.mx/documents/ejercicio-resueltos-cables.html
No hay comentarios:
Publicar un comentario